std::chi_squared_distribution(C++11)

namespace std {
  template <class RealType = double>
  class chi_squared_distribution;
}

概要

chi_squared_distributionは、乱数をカイ二乗分布(χ二乗分布、χ²分布)させるクラスである。以下の確率密度関数に基いて、浮動小数点数の乱数を生成する。

$$ p(x \mid n) = \frac{x^{n/2 - 1} \cdot e^{-x/2}}{\Gamma (n/2) \cdot 2^{n/2}} $$

この確率密度関数において、nは自由度(degrees of freedom)を意味する。

カイ二乗分布は、以下のような用途に使用できる：

赤玉20個、白玉20個が混ざった箱から、20個の玉を取り出す。その際の、期待値(赤玉10個、白玉10個)からのずれの度合いを判定する。
異なる世代で、1ヶ月に利用する携帯電話の利用時間に差が出るか判定する。
これらの用途を一般化すると、χ²検定(chi-square test)やフリードマン検定(Friedman test)といった科学的検定に分類される。

上記の例では、自由度は1となる(玉の種類(2) - 1)。玉の種類が3の場合は自由度2になる。

テンプレートパラメータは、以下を意味する：

RealType : 生成する実数の型。

メンバ関数

構築・リセット

名前	説明	対応バージョン
`(constructor)`	コンストラクタ	C++11
`~chi_squared_distribution() = default;`	デストラクタ	C++11
`reset`	状態をリセットする	C++11

生成

名前	説明	対応バージョン
`operator()`	乱数を生成する	C++11

プロパティ

名前	説明	対応バージョン
`n`	分布の自由度を取得する	C++11
`param`	分布のパラメータを取得／設定する	C++11
`min`	生成し得る値の下限を取得する	C++11
`max`	生成し得る値の上限を取得する	C++11

メンバ型

型	説明	対応バージョン
`result_type`	乱数生成結果の実数型 `RealType`。	C++11
`param_type`	分布パラメータの型。未規定。	C++11

非メンバ関数

名前	説明	対応バージョン
`operator==`	等値比較	C++11
`operator!=`	非等値比較	C++11
`operator<<`	ストリームへの出力	C++11
`operator>>`	ストリームからの入力	C++11

例

#include <fstream>
#include <random>

int main()
{
  std::random_device seed_gen;
  std::default_random_engine engine(seed_gen());

  // 自由度1で分布させる
  std::chi_squared_distribution<> dist(1.0);

  std::ofstream file("chi_squared_distribution.tsv");
  for (size_t n = 0; n < 1024; ++n) {
    // カイ二乗分布で乱数を生成する
    double result = dist(engine);
    file << result << "\n";
  }
}

出力

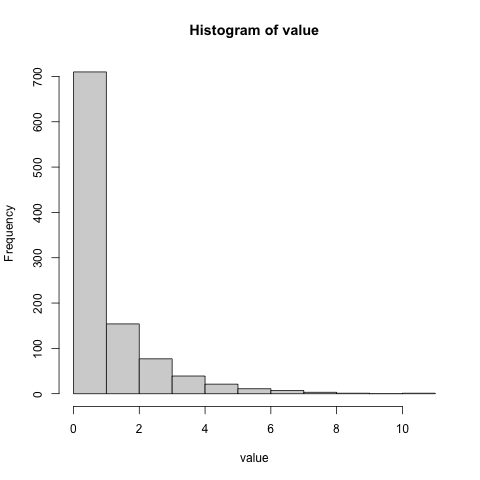
このプログラムによってある時に得られた結果（chi_squared_distribution.tsv）を図示する。