random

<random>ヘッダは、擬似乱数を取り扱うための乱数生成器 (Random Number Generator) や分布生成器 (Distribution) 、非決定論的な乱数生成器、および関連する一連のクラス・関数を定義する乱数ライブラリである。

このヘッダでは、以下の標準ヘッダをインクルードする：

• <initializer_list>

コンセプト

擬似乱数生成器

擬似乱数生成器は、ソフトウェアで乱雑な値のシーケンスを生成するクラスである。

擬似乱数生成器は、環境によらず同じシードを与えれば同じ乱数列が生成される。

多くのユーザーにとっては、以下に挙げる生の乱数生成器テンプレートクラスそのものよりも、後述するパラメータ定義済みの乱数生成器の型を使用すれば十分である。

生成器アダプタ

生成器アダプタは、他の乱数生成器の乱数列を調整するクラスである。

通常、ユーザーがこれらのクラスを直接使用することはない。新たな乱数アルゴリズムを作る上級者、および研究者向けの機能である。

パラメータ定義済み擬似乱数生成器

先に挙げた擬似乱数生成器に対して一般的なパラメータを定義し、使いやすいように用意された擬似乱数生成器の型。

これらの型には、パフォーマンス、オブジェクトのサイズ、周期などのトレードオフがある。ユーザーの目的に合わせて擬似乱数生成器の型を選択してほしい。

オブジェクトのサイズをある程度無視・許容できる状況では、多くの分野と用途に、mt19937を推奨できる。

非決定論的な乱数生成器

擬似乱数には「予測できる」「再現性がある」という特徴がある。

暗号化、パスワードの生成、擬似乱数のシードを決定するといった、エンドユーザーに予測されたくない乱数列が必要な場合に、擬似乱数の代わりに、以下の非決定論的な乱数生成器を利用できる。

シード数列

分布生成器

分布生成器は、乱数生成器によって生成される値の範囲や分布を調整するクラスである。

分布生成器は、環境によって異なるアルゴリズムで実装される可能性がある。擬似乱数生成器は環境によらず同じシードを与えれば同じ乱数列が生成されるが、分布生成器を介して乱数生成する場合、環境によって異なる乱数列が生成される場合がある。

一様分布

ベルヌーイ分布(Bernoulli Distribution)

ポワソン分布(Poisson Distribution)

正規分布(Normal Distribution)

標本分布(Sampling Distribution)

ユーティリティ

例

以下に示す例では、標準の乱数ライブラリを用いてランダムデバイスでシードを生成してメルセンヌツイスタエンジンを初期化、単精度浮動小数点数型で区間[-1.0f, 1.0f)の一様分布、および1.0fを中心として標準偏差0.5fの正規分布に基づく擬似乱数を100万個生成し"random.tsv"にタブ区切り形式のファイルとして結果を保存する。

#include <fstream>
#include <random>

int main()
{
  // メルセンヌ・ツイスター法による擬似乱数生成器を、
  // ハードウェア乱数をシードにして初期化
  std::random_device seed_gen;
  std::mt19937 engine(seed_gen());

  // 一様実数分布
  // [-1.0f, 1.0f)の値の範囲で、等確率に実数を生成する
  std::uniform_real_distribution<float> dist1(-1.0f, 1.0f);

  // 正規分布
  // 平均1.0f、標準偏差0.5fで分布させる
  std::normal_distribution<float> dist2(1.0f, 0.5f);

  std::ofstream file("random.tsv");
  for (size_t i = 0; i < 1000*1000; ++i) {
    // 各分布法に基いて乱数を生成
    float r1 = dist1(engine);
    float r2 = dist2(engine);

    file << r1 << "\t" << r2 << "\n";
  }
}

xxxxxxxxxx

#include <fstream>

#include <random>

​

int main()

{

  // メルセンヌ・ツイスター法による擬似乱数生成器を、

  // ハードウェア乱数をシードにして初期化

  std::random_device seed_gen;

  std::mt19937 engine(seed_gen());

​

  // 一様実数分布

  // [-1.0f, 1.0f)の値の範囲で、等確率に実数を生成する

  std::uniform_real_distribution<float> dist1(-1.0f, 1.0f);

​

  // 正規分布

  // 平均1.0f、標準偏差0.5fで分布させる

  std::normal_distribution<float> dist2(1.0f, 0.5f);

​

  std::ofstream file("random.tsv");

  for (size_t i = 0; i < 1000*1000; ++i) {

    // 各分布法に基いて乱数を生成

    float r1 = dist1(engine);

    float r2 = dist2(engine);

​

    file << r1 << "\t" << r2 << "\n";

  }

}

​

この例である時得られた random.tsv (ファイルサイズが大きいので添付する上では random.tsv.xz に圧縮) を元に、得られたデータの密度を図示すると、以下のような図が得られた。

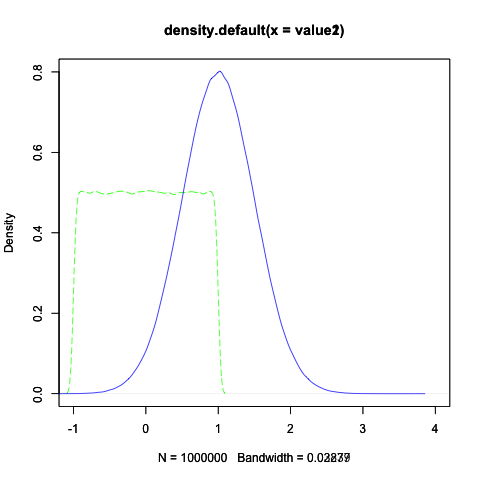
破線は dist1 (一様分布; min=-1.0f, max=1.0f) 、実線は dist2 (正規分布; mean=1.0f, stdev=0.5f) 、横軸は値、縦軸は密度(値の件数を区間ごとに数えたヒストグラムを全体に占める割合で表したもの)である。

標準乱数ライブラリの基本的な使い方

「擬似」乱数生成器

擬似乱数生成器は決定論的で、再現性を持つ。 擬似乱数生成器に同じシードを与えることで、同じ乱数列を再現させられる。この挙動は開発中のテストやデバッグなどで有用である。 実行ごとに異なる乱数列が必要な場合、random_device クラスのような非決定論的に実装される乱数をシードとして使用するとよい。

また、擬似乱数生成器は高速かつ高効率に動作するよう設計されている。 しかしながら、これらが生成する乱数列は真の乱数ではなく、周期を持つ。

<random> が提供する擬似乱数生成器は暗号論的に安全ではない。

一方 random_device は非決定論的である（ただし実装は処理系定義なので詳細は項目を参照すること）が、 速度は擬似乱数生成器に比べ遅く、特にエントロピープールが枯渇すると著しく悪化する。

モンテカルロ法など多数の乱数が必要な場合は擬似乱数生成器の使用を推奨する。

推奨する擬似乱数エンジン

基本的には32ビット版メルセンヌ・ツイスターの実装であるmt19937、もしくはその64ビット版の実装であるmt19937_64のどちらかを使用することを推奨する。

非専門用途のためのdefault_random_engineというエンジン型も定義されているが、この型は環境によって乱雑度が低く、周期も短い擬似乱数エンジンの別名として定義される場合がある。

mt19937は、状態の大きさがsizeof(std::uint_fast32_t) * (624 + 1)だけあり、少々サイズが大きいが、それを受け入れられる状況であれば、デフォルトでmt19937を採用しよう。このエンジンでは、乱雑度や周期の長さが問題になることは少ない。

特定の範囲の整数や浮動小数点数が必要な場合

uniform_int_distributionやuniform_real_distributionのような、専門特化した分布クラスを使用する。

古典的な方法として、特定の範囲の整数を生成するために、剰余演算が使われていた。たとえば[0, 6)の範囲のランダムな整数が必要な場合には、int x = random_value % 6;のようにしていた。この方法では、modulo biasと呼ばれる値の偏り問題が発生する。この場合は、[0, 3]の値が出力される確率が17%で、[4, 5]の値が出力される可能性は16%となり、小さい値の方が確率が高くなる。これは、出力される可能のある乱数の最大値が、剰余する値で割り切れない場合に発生する偏りである。

専門特化した一様分布のクラスを使用することで、そのような偏りは起こらなくなる。

シード生成法

リリース版においては、実行ごとに擬似乱数のシードが異なることが求められる。 random_device クラスが非決定論的に実装されている環境ではこれを使用するのが望ましい。

古典的な方法として、シードにはstd::time(NULL)で取得した現在時間 (エポックからの経過秒) が使われてきた。 しかしながら、この方法ではアプリケーションの起動時間によってシードを調整され、乱数列を制御されてしまう。

これを防ぐには、非決定論的な random_device や CPU の RDRAND 命令などを使用してシードを生成するのがよいだろう。

バージョン

言語

• C++11

参照

分布アルゴリズム

• さまざまな確率分布 (probability distributions)
• 確率変数－種々の分布の特徴

乱数ライブラリの使い方

• N3551 Random Number Generation in C++11
• Pitfalls in Random Number Generation

乱数ライブラリが導入された経緯

• N0352 Proposal for Standardization of Random Number Generators in C++
• N1398 A Proposal to Add an Extensible Random Number Facility to the Standard Library
• N1452 A Proposal to Add an Extensible Random Number Facility to the Standard Library (Revision 2)
• N1588 On Random-Number Distributions for C++0x
• N1837 Library Extension Technical Report  Issues List
• N1914 A Proposal to Add Random-Number Distributions to C++0x
• N1932 Random Number Generation in C++0X: A Comprehensive Proposal
• N1933 Improvements to TR1’s Facility for Random Number Generation
• N2032 Random Number Generation in C++0X: A Comprehensive Proposal, version 2
• N2033 Proposal to Consolidate the Subtract-with-Carry Engines
• N2079 Random Number Generation in C++0X: A Comprehensive Proposal, version 3
• N2111 Random Number Generation in C++0X: A Comprehensive Proposal, version 4
• N2423 Recommendations for Resolving Issues re [rand], Version 2
• N2424 Recommendations for Resolving the 2007-09-21 Issues re [rand]

その他

• N2930 Range-Based For Loop Wording (Without Concepts)

編集者向けの参照

• 乱数分布の図を作る方法