std::fisher_f_distribution(C++11)

namespace std {
  template <class RealType = double>
  class fisher_f_distribution;
}

概要

fisher_f_distributionは、連続確率分布の一種である、フィッシャーのF分布を生成するクラスである。以下の確率密度関数に基いて、浮動小数点数の乱数を生成する：

$$ p(x \mid m, n) = \frac{\Gamma ((m+n)/2)}{\Gamma (m/2) \Gamma (n/2)} \cdot \left( \frac{m}{n} \right) ^{m/2} \cdot x^{(m/2)-1} \cdot \left( 1 + \frac{mx}{n} \right) ^{-(m+n)/2} $$

この確率密度関数におけるmとnは自由度(degrees of freedom)で、2つの独立したカイ二乗分布を除算したものを結果として生成する。

以下のような用途で使用できる：

2つの標本の分散比を求める。

テンプレートパラメータは、以下を意味する：

RealType : 生成する実数の型。

メンバ関数

構築・リセット

名前	説明	対応バージョン
`(constructor)`	コンストラクタ	C++11
`~fisher_f_distribution() = default;`	デストラクタ	C++11
`reset`	状態をリセットする	C++11

生成

名前	説明	対応バージョン
`operator()`	乱数を生成する	C++11

プロパティ

名前	説明	対応バージョン
`m`	分布の自由度mを取得する	C++11
`n`	分布の自由度nを取得する	C++11
`param`	分布のパラメータを取得／設定する	C++11
`min`	生成し得る値の下限を取得する	C++11
`max`	生成し得る値の上限を取得する	C++11

メンバ型

型	説明	対応バージョン
`result_type`	乱数生成結果の実数型 `RealType`。	C++11
`param_type`	分布パラメータの型。未規定。	C++11

非メンバ関数

名前	説明	対応バージョン
`operator==`	等値比較	C++11
`operator!=`	非等値比較	C++11
`operator<<`	ストリームへの出力	C++11
`operator>>`	ストリームからの入力	C++11

例

#include <fstream>
#include <random>

int main()
{
  std::random_device seed_gen;
  std::default_random_engine engine(seed_gen());

  // 自由度5と10で分布させる
  std::fisher_f_distribution<> dist(5, 10);

  std::ofstream file("fisher_f_distribution.tsv");
  for (std::size_t n = 0; n < 256; ++n) {
    // F分布で乱数を生成する
    double result = dist(engine);
    file << result << "\n";
  }
}

出力

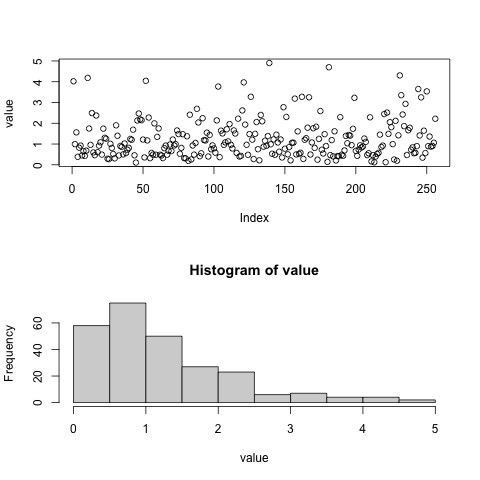
このプログラムによってある時に得られた結果（fisher_f_distribution.tsv）を図示する。