std::cauchy_distribution(C++11)

namespace std {
  template <class RealType = double>
  class cauchy_distribution;
}

概要

cauchy_distributionは、連絡確率分布の一種であるコーシー分布(ローレンツ分布とも呼ばれる)を生成するクラスである。
正規分布(normal_distribution)と違い、平均も分散も定義されない、という特徴を持つ。
以下の確率密度関数に基いて、浮動小数点数の乱数を生成する：

$$ p(x \mid a, b) = \left( \pi b \left(1 + \left( \frac{x-a}{b} \right) ^2 \right) \right) ^{-1}$$

この確率密度関数において、aは分布の最頻値を与える位置母数(location parameter)、bは半値半幅を与える尺度母数(scale parameter)である。

コーシー分布は、以下のような用途に使用できる：

正規分布に比べて外れ値(outliers)が非常に多い場合の分布のモデル
原子核物理の分野において、放射線の線スペクトルの強度分布などの共鳴現象(この分野では、ブライト・ウィグナー分布とも呼ばれている)

テンプレートパラメータは、以下を意味する：

RealType : 成功する実数の型。

メンバ関数

構築・リセット

名前	説明	対応バージョン
`(constructor)`	コンストラクタ	C++11
`~cauchy_distribution() = default;`	デストラクタ	C++11
`reset`	状態をリセットする	C++11

生成

名前	説明	対応バージョン
`operator()`	乱数を生成する	C++11

プロパティ

名前	説明	対応バージョン
`a`	分布の位置母数を取得する	C++11
`b`	分布の尺度母数を取得する	C++11
`param`	分布のパラメータを取得／設定する	C++11
`min`	生成し得る値の下限を取得する	C++11
`max`	生成し得る値の上限を取得する	C++11

メンバ型

型	説明	対応バージョン
`result_type`	乱数生成結果の整数型。`IntType`	C++11
`param_type`	分布パラメータの型。未規定。	C++11

非メンバ関数

名前	説明	対応バージョン
`operator==`	等値比較	C++11
`operator!=`	非等値比較	C++11
`operator<<`	ストリームへの出力	C++11
`operator>>`	ストリームからの入力	C++11

例

#include <fstream>
#include <random>

int main()
{
  std::random_device seed_gen;
  std::default_random_engine engine(seed_gen());

  // 位置母数0.0、尺度母数1.0で分布させる
  std::cauchy_distribution<> dist(0.0, 1.0);

  std::ofstream file("cauchy_distribution.tsv");
  for (std::size_t n = 0; n < 1000; ++n) {
    // コーシー分布で乱数を生成する
    double result = dist(engine);
    file << result << "\n";
  }
}

出力

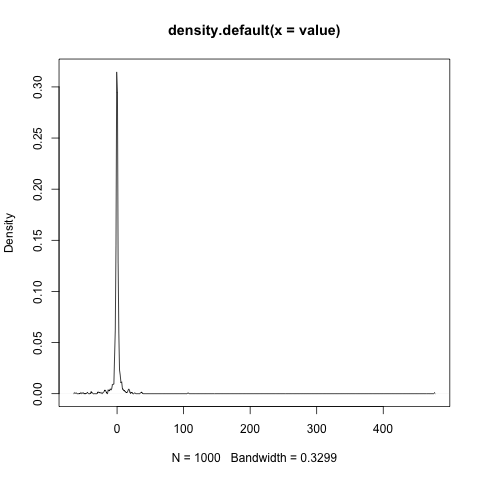
このプログラムによってある時に得られた結果（cauchy_distribution.tsv）を図示する。