4. atan2

最終更新日時(UTC):
が更新

履歴 編集

function
<cmath>

std::atan2

namespace std {
  float atan2(float y, float x);          // (1) C++03からC++20まで
  double atan2(double y, double x);       // (2) C++03からC++20まで
  long double
    atan2(long double y, long double x);  // (3) C++03からC++20まで

  floating-point-type
    atan2(floating-point-type y,
          floating-point-type x);         // (4) C++23
  constexpr floating-point-type
    atan2(floating-point-type y,
          floating-point-type x);         // (4) C++26

  Promoted
    atan2(Arithmetic1 y,
          Arithmetic2 x);                 // (5) C++11
  constexpr Promoted
    atan2(Arithmetic1 y,
          Arithmetic2 x);                 // (5) C++26

  float
    atan2f(float y, float x);             // (6) C++17
  constexpr float
    atan2f(float y, float x);             // (6) C++26

  long double
    atan2l(long double y, long double x); // (7) C++17
  constexpr long double
    atan2l(long double y, long double x); // (7) C++26
}

概要

算術型の逆正接（アークタンジェント）を対辺と隣辺から求める。

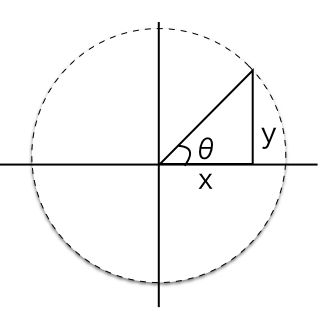
このような三角形があった場合、辺yの長さと辺xの長さをatan2()関数に与えることで、角度θがラジアン単位として求まる。

戻り値

y / x の逆正接を [-π, π] の範囲で返す。（単位はラジアン）

象限は引数の符号から適切に求められる。

yとxの両方が値0である場合に定義域エラーとなる可能性がある。定義域エラーが発生した場合、戻り値は処理系定義である。（備考参照）

備考

  • $$ f(y, x) = \mathrm{Arctan}~\frac{y}{x} $$

    引数の順番に注意されたし。

  • 定義域エラーが発生した場合の挙動については、<cmath> を参照。

  • C++11 以降では、処理系が IEC 60559 に準拠している場合（std::numeric_limits<T>::is_iec559() != false）、以下の規定が追加される。（複号同順）

    • y = ±0 で x < 0 または x = -0 の場合、戻り値は ±π となる。
    • y = ±0 で x > 0 または x = +0 の場合、戻り値は ±0 となる。
    • y > 0 で x = ±0 の場合、戻り値は +π/2 となる。
    • y < 0 で x = ±0 の場合、戻り値は -π/2 となる。
    • 0 < z < +∞ とすると、y = ±z で x = -∞ の場合、戻り値は ±π となる。
    • 0 < z < +∞ とすると、y = ±z で x = +∞ の場合、戻り値は ±0 となる。
    • y = ±∞ で x が有限の値の場合、戻り値は ±π/2 となる。
    • y = ±∞ で x = -∞ の場合、戻り値は ±3π/4 となる。
    • y = ±∞ で x = +∞ の場合、戻り値は ±π/4 となる。

    特に、y と x の両方がゼロの場合に定義域エラー（FE_INVALID（無効演算浮動小数点例外））となったり、y が非ゼロで x がゼロの場合に極エラー（FE_DIVBYZERO（ゼロ除算浮動小数点例外））となったりはしない事に注意。

  • C++23では、(1), (2), (3)が(4)に統合され、拡張浮動小数点数型を含む浮動小数点数型へのオーバーロードとして定義された

例

#include <cmath>
#include <iostream>

int main() {
  std::cout << std::fixed;
  std::cout << "atan2(0.0, 1.0)   = " << std::atan2(0.0, 1.0) << std::endl;
  std::cout << "atan2(1.0, 1.0)   = " << std::atan2(1.0, 1.0) << std::endl;
  std::cout << "atan2(1.0, 0.0)   = " << std::atan2(1.0, 0.0) << std::endl;
  std::cout << "atan2(1.0, -1.0)  = " << std::atan2(1.0, -1.0) << std::endl;
  std::cout << "atan2(0.0, -1.0)  = " << std::atan2(0.0, -1.0) << std::endl;
  std::cout << "atan2(-1.0, -1.0) = " << std::atan2(-1.0, -1.0) << std::endl;
  std::cout << "atan2(-1.0, 0.0)  = " << std::atan2(-1.0, 0.0) << std::endl;
  std::cout << "atan2(-1.0, 1.0)  = " << std::atan2(-1.0, 1.0) << std::endl;
}

出力

atan2(0.0, 1.0)   = 0.000000
atan2(1.0, 1.0)   = 0.785398
atan2(1.0, 0.0)   = 1.570796
atan2(1.0, -1.0)  = 2.356194
atan2(0.0, -1.0)  = 3.141593
atan2(-1.0, -1.0) = -2.356194
atan2(-1.0, 0.0)  = -1.570796
atan2(-1.0, 1.0)  = -0.785398

バージョン

言語

  • C++03

処理系

  • Clang: 1.9 ✅, 2.9 ✅, 3.1 ✅
  • GCC: 3.4.6 ✅, 4.2.4 ✅, 4.3.5 ✅, 4.4.5 ✅, 4.5.1 ✅, 4.5.2 ✅, 4.6.1 ✅, 4.7.0 ✅
  • ICC: 10.1 ✅, 11.0 ✅, 11.1 ✅, 12.0 ✅
  • Visual C++: 2003 ✅, 2005 ✅, 2008 ✅, 2010 ✅

備考

特定の環境では、早期に constexpr 対応されている場合がある：

  • GCC 4.6.1 以上

実装例

[-π/2, π/2] の範囲を返す atan があれば、引数の符号に応じて以下のように変換することで求められる。

$$ \mathrm{Arctan}~\frac{y}{x} = \begin{cases} \displaystyle \mathrm{Arctan}~\frac{y}{x} & \quad \mathrm{for} \; 0 \le x \\[2ex] \displaystyle \mathrm{Arctan}~\frac{y}{x} + \pi & \quad \mathrm{for} \; x < 0, \; 0 \le y \\[2ex] \displaystyle \mathrm{Arctan}~\frac{y}{x} - \pi & \quad \mathrm{for} \; x < 0, \; y < 0 \end{cases} $$

参照